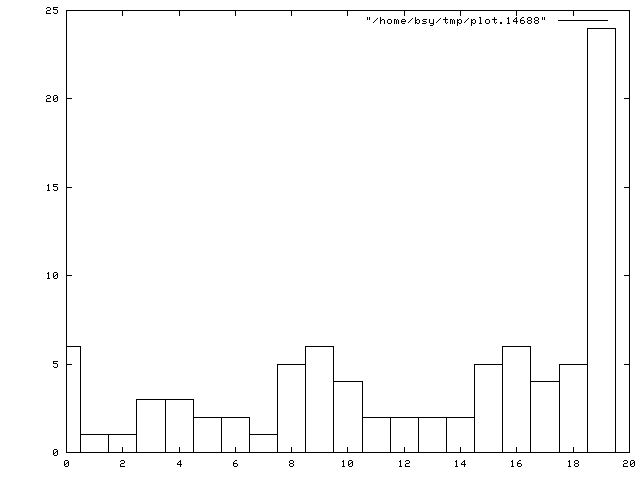
About the grading:
; exp.oic
;
; CSE 30 Fall 97, Assignment #2: sample solution.
; Stephane Belmon, October 1997.
;
; Requirements: the answer has to compute x^y for non-negative integers,
; including 0^y and x^0. Overflows are to be ignored. It must use a
; subroutine for the multiplication.
;
; Assumptions:
; x is a unsigned integer stored at 0x1000
; y is a unsigned integer stored at 0x1001
; The result will be stored at 0x1002
;
; 0^0 is 1, 0^y is 0 for y>0, x^0 is 1, overflows ignored.
;
; Usage:
; "oic -s 0x1000 -c 3 exp.oic test1.oic"
; The last line of the dump will show the result (in hexadecimal).
;
; See the attached "test*.oic" files for the test suite.
;
; The equivalent C code is:
;
; p = 1;
; i = -y;
; while (i != 0) {
; p = mult(p,x);
; i = i + 1;
; }
;
; The mult subroutine is as given in
; http://www-cse.ucsd.edu/classes/fa97/cse30/handouts/mult.oic
; We implement the parameter passing by simply storing the two parameters
; in the variables a and b, and we store the multiplication result in c.
;
; The number right after the ";" is a reminder of the current address
; (hex) (for lines that have a triplet).
;
0
0x1002 0x1002 0x1 ;0 exp: subz p,p,next
0x1002 0x29 0x2 ;1 subz p,neg1,next p = 1;
0x26 0x26 0x3 ;2 subz i,i,next
0x26 0x1001 0x4 ;3 subz i,y,next i = -y;
0x26 0x28 0x17 ;4 mloop: subz i,zero,mdone while (i != 0) {
; -- prepare to call mult
0x22 0x22 0x6 ;5 subz t,t,next
0x22 0x1002 0x7 ;6 subz t,p,next
0x23 0x23 0x8 ;7 subz a,a,next
0x23 0x22 0x9 ;8 subz a,t,next a = p;
0x22 0x22 0xa ;9 subz t,t,next
0x22 0x1000 0xb ;a subz t,x,next
0x24 0x24 0xc ;b subz b,b,next
0x24 0x22 0xd ;c subz b,t,next b = x;
0x21 0x21 0xe ;d subz multret,multret,next -- prepare return
0x21 0x2a 0xf ;e subz multret,retproto,next
0x21 0x2b 0x10 ;f subz multret,negretmultr,next
0x22 0x22 0x18 ;10 subz t,t,mult -- call
;retmultr: -- return point
0x22 0x22 0x12 ;11 subz t,t,next
0x22 0x25 0x13 ;12 subz t,c,next
0x1002 0x1002 0x14 ;13 subz p,p,next
0x1002 0x22 0x15 ;14 subz p,t,next p = c;
0x26 0x29 0x16 ;15 subz i,neg1,next i = i+1;
0x22 0x22 0x4 ;16 subz t,t,mloop }
;
0x22 0x22 0x17 ;17 mdone: subz t,t,mdone -- infinite loop (exit)
;
;
; Mult subroutine: computes a*b
;
; Assumptions:
; The parameters are stored in a and b.
; The result will be stored in c.
; The return instruction has to be generated and written at "multret:"
; before the caller jumps to "mult:"
;
; Side-effects:
; This routine will use j and t as scratch. a and b are read only.
;
0x27 0x27 0x19 ;18 mult: subz j,j,next
0x27 0x23 0x1a ;19 subz j,a,next j = -a;
0x22 0x22 0x1b ;1a subz t,t,next t = 0;
0x27 0x28 0x1f ;1b loop: subz j,zero,loop_done while (j!=0) {
0x22 0x24 0x1d ;1c subz t,b,next t = t-b;
0x27 0x29 0x1e ;1d subz j,neg1,next j = j+1;
0x28 0x28 0x1b ;1e subz zero,zero,loop }
; loop_done:
0x25 0x25 0x20 ;1f subz c,c,next
0x25 0x22 0x21 ;20 subz c,t,next c = -t;
; multret:
0 0 0 ;21 0 0 0 -- generated return instruction here
;
; Data
;
0 0 0 ;22 t: 0 0 0 -- scratch in various places
0 0 0 ;23 a: 0 0 0 -- parameter for mult subroutine
0 0 0 ;24 b: 0 0 0 -- parameter for mult subroutine
0 0 0 ;25 c: 0 0 0 -- result of mult subroutine
0 0 0 ;26 i: 0 0 0 -- main (exp) loop counter
0 0 0 ;27 j: 0 0 0 -- mult loop counter
;
; Constants
;
0 0 0 ;28 zero: 0 0 0
0xffff 0xffff 0xffff ;29 neg1: 0xffff 0xffff 0xffff -- is -1
0xffdd 0xffde 0x0000 ;2a retproto: 0xffdd 0xffde 0x0000 ; - (t t 0)
; -- general return instruction prototype,
; -- opposite of "subz t, t, 0"
; -- - 0x002200220000 == 0xffddffde0000
; -- (t is at 0x22)
0xffff 0xffff 0xffef ;2b negretmultr: 0xffff 0xffff 0xffef
; -- Opposite of the return point address
; -- in the main loop.
; -- The return point is 0x11
; -- so negretmultr contains 0xffffffffffef
This solution was not written to be efficient, but it is (I hope)
clear. It would be possible to save some instructions by merging
a and p, and by using c instead of the
temporary t in the mult subroutine. However, this
"sub-optimal" version clearly separates the arguments from the
temporary variables used for the computations.
Please note the "assumptions" and "side-effects" comments for the mult subroutine. These comments are very useful for the user of the subroutine (why ?). In MIPS assembly language, some side-effects are "implicit", like trashing the $t registers, but you should make most other things explicit. These comments are much more useful than explaining in English that you "initialize a variable to zero by substracting it from itself", which is obvious from the code. Remember that comments are intended to help a programmer who knows well the language (here OIC), but who doesn't know what you are trying to do.
For an explanation of the process of converting from subzs to machine language form (hex) , ie "assembling", please refer to this part of lecture 4.
See lecture 4 for an explanation of the call sequence (self-modifying code).
You could also have written a solution with an add subroutine called by the mult subroutine. It was not required and it is slightly more complicated (good: you learned more). In such a case, you would have to take care of generating two distinct return instructions. You would have two negated return point addresses: one for the return point in the main loop, one for the return point in the mult loop. But you would have only one retproto .
Grading statistics are:
86 students handed in something.
Assignment as a whole: mean 63.8908
stdev 32.4561
Part 1: mean 26.872093
stdev 12.713110
Part 2: mean 25.000000
stdev 17.620020
Part 3: mean 14.104651
stdev 7.512825
The grade distribution was:

bsy@cse.ucsd.edu, last updated